Last time we looked at some good reasons why using the formula makes sense when trying to describe screen shapes, and co-ordinating content on to them.
Now we’ll take a detailed look at an example applying the formula to Christie Digital’s innovative new modular screen display system, MicroTiles, which has just been announced.
Shown below is one of the screen shapes which was on display at the launch party at Touch nightclub in Manhattan this week, the tiles forming a custom shaped screen with a surround detailing the screen edges.

A skyscraper made of MicroTiles
This particular screen shape was called ‘skyscraper’, i.e. with reference to a city’s skyline and a whole mixture of clever content was designed especially for this screen.
The image shown was one small part of a dynamic sequence, and you can clearly see that the design elements have been carefully crafted to make the best possible use of this particular (screen) shape.
So how do we describe this screen with the formula? Just giving it a name ‘skyscraper’ does not help the content or AV people when putting the whole thing together.
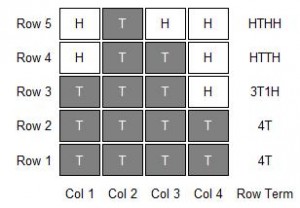
Thinking back to our squared paper example with tile (T) and hole (H) elements, and counting from the bottom left, we look at each row and produce a term describing what we have in each column for that row.
The skyscraper re-defined
There are two types of row definition, a short and long one. The long definition lists each screen element with a single letter, so the bottom row in this case would be “TTTT”.
All well and good for smaller screen arrays, but what about big screens with, say, 16 tiles across? You start to get an awful lot of letters, and that’s just for one row.
So the short version allows you to summarise the number of continuous elements in a row with a number, so in a 16 tile row it would reduce to “16T”, or in the case of this Skyscraper, “4T”.
Geek alert: the more technically minded will recognise this method as run-length encoding – hopefully we’ve kept it simple enough here to be easily understood, Ed
A side effect of using the short row definition is that shorter rows with different screen elements could actually take longer to describe than using the long definition – in the Skyscraper, row 4 is shown here as “HTTH” (long definition), but using the short definition it becomes “1H2T1H” which ends up slightly longer!
This is why we have both types, and each row term can use either long or short version as appropriate in the same formula for the overall screen. In the diagram above, we have used the short version for rows 1-3, and the long version in rows 4 and 5.
So for each row we produce a term of letters (and sometimes numbers) which describe the row. See the diagram for the row term for each row in this Skyscraper screen.
Then we put them together in order, starting with row 1 (from the bottom up) with an underscore character between each one.
At the start of the code, we put the number of screen elements of the overall square shape bounding the screen, with the letter X between them.
So starting from bottom left again, there are 4 across by 5 up, making it “4X5”.
This term goes at the front of the code, and tells you two useful things:-
- the overall size of the screen (depending on what technology your screen elements are)
- the aspect ratio that the screen is
Assuming a standard aspect video image is displayed over the whole screen area, you can then tell if the image will be stretched anamorphically or not – if the screen is a 1X3, then the image will be stretched vertically, for example.
Putting it all together, all this makes the complete formula for this Skyscraper screen example: _4X5_4T_4T_3T1H_HTTH_HTHH_
As implied in the previous posts, see The ‘Issy-Neale Formula’ Explained Part 1 and The ‘Issy-Neale Formula’ Explained Part 2, this sequence of characters can now be used at whatever level you like in your planning, content creation, scheduling, and distribution processes.
- Those with the capability for custom software development can use it to automatically sort content for scheduling and distribution.
- Those who want to keep up a good level of co-ordination between third parties could standardise on using the formula in their business processes to make sure everyone knows exactly what they are talking about when dealing with screen shapes.
- Those who are designing bespoke content for different shapes can attach the formula to the filenames, folders or other database-style meta data for each piece of content.
The ‘Issy-Neale Formula’ Explained Part 1
The ‘Issy-Neale Formula’ Explained Part 2
The ‘Issy-Neale Formula’ Explained Part 3

November 16th, 2009 at 08:21 @390
Lose the 1 in 1H2T1H – it’s not adding anything. Then you can describe the row as H2TH for greater clarity.
November 16th, 2009 at 11:08 @505
Our aim was to create something that was both easily human-readable and machine-readable, and to keep it well structured, but also as simple as possible.
If we were to drop the 1 in the 1H2T1H term, it would effectively be mixing the short and long definitions in the same row term. I agree that it would be easier to read and interpret from a human point of view, but it would make machine-readable parsing more difficult (although obviously not impossible), and in the interests of simple structure and conformity, we decided that it was best not to mix the two within an individual row term.
January 13th, 2012 at 15:04 @669
So far, so good… But is there any provision for orientation of the display/projector elements?
For example, all of the elements might be landscape, all might be portrait, or there may be a mixture in the overall wall. Worst case (if the designers had complete reign!), there could also be mixtures of elements with different resolutions (1366 x 768 vs. 1980 x 1080) or even different aspect ratios (much less likely if the system designers get a say!).